CAD/CAMを中心としたソフトウェアの企画・開発でお客様のニーズに合わせたコンピュータ活用を支援します。

NURBSとはNon Uniform Rational B Splineのことです。直訳すれば、一様でなくて（ノンユニフォーム）有理な（ラショナル）Bスプラインとなります。
NURBS曲線・曲面を象徴的に描くと次のようになります。

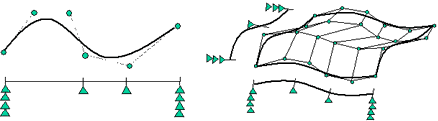
図11 NURBS曲線とNURBS曲面（制御点とノットを象徴的に表示）

1 NURBSを記述する要素

NURBS（ナーブス）曲線は次の4つの要素から記述されます。ここでは、特に断らない限りここでは曲線について説明します。詳細や曲面は、最終章の文献を参照してください。

<階数（次数）>

NURBS曲線は、xyz空間に描かれたn次式のグラフです。次数という概念が登場します。次数に1を加えた値を階数と呼びます。曲率まで曲線の滑らかさを制御するためには、階数として4（次数3）で十分です。

<ノットベクトル>

Bスプライン基底関数を決定するためのパラメータです。（階数＋制御点数）個の単調増加する数列です。

図12 制御点とノットベクトル

2 Bスプライン基底関数とBスプライン曲線

Bスプライン基底関数Nj(t)は、パラメータtの増加とともに、普段は0なのですが、ある範囲だけプラスの値を取ります。プラスの値は徐々に大きくなり徐々に小さくなります。

図13 ノットベクトルとあるBスプライン基底関数

制御点1個につき1個のBスプライン基底関数が割り当てられます。あるtのとき個々の基底関数の値は、担当している制御点の影響の強さをあらわしています。基底関数がピークを迎えるtは、制御点の順番にそって少しずつずれています。

図14 全ての制御点と基底関数（制御点数6の場合）

あるtのときのBスプライン曲線上の点は、この制御点の影響がバランスする位置に求められます。バランスする位置は、パラメータtの増加とともに最初の制 御点から最後の制御点の方へ移っていきます。Bスプライン曲線は、バランスした位置を全てのパラメータについてプロットしたものです。

図16 パラメータtが増加すると影響する制御点とともにバランスする位置がずれていく

ノットベクトルは、個々の基底関数がプラスの値になる範囲やピークを迎える時期を決定します。

3 ノンユニフォーム（非一様）

ノットベクトルの間隔は適当に指定することができます。等間隔（一様：ユニフォーム）ですと基底関数の山の形は担当する制御点にかかわらず同じになります。等間隔にしない（非一様：ノンユニフォーム）と山の形が尖ったりなだらかになったりします。

図17 ノットベクトルと基底関数の形

4 ラショナル（有理）

あるパラメータtにおける各制御点の影響力は、割り当てられた基底関数が決定しています。もうひとつ影 響力を決定する要素があります。制御点に与えられたウェイトwです。ウェイトwが大きいと影響力も大きくなり、描かれたBスプライン曲線はその制御点の近 くを通ります。ウェイトwの調整を利用すると、放物線にしかならない階数3（次数2）の曲線が、誤差なく円弧をあらわせるようになります。
CADユーザが意識しているのは3次元空間で（x､y､z）の世界です。NURBSは、ウェイトが加わった4次元空間（x,y,z,w）で描かれています。ラショナル（有理）とは、この4次元空間で考えているということです。

図18 制御点のウェイトとBスプライン曲線の形

5 NURBS曲線をあらわす式

制御点Qj、ウェイトwj、Bスプライン基底関数Nj（t）を用いて次のような計算をするとパラメータ （t）からP（x,y,z）が求まります。Bスプライン基底関数Nj(t)が制御点Qjの影響力を決めていること、ウェイトwが分母にあらわれるので有理 式であることなどがわかりますね。